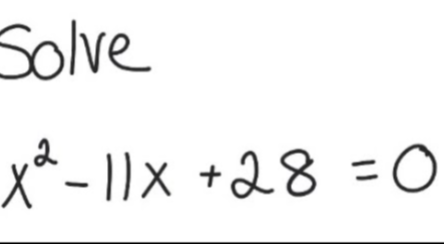
Introduction
In the realm of mathematics, equations are the building blocks of problem-solving. One such equation that often piques curiosity is X2-11X+28=0. This seemingly enigmatic arrangement of symbols holds the key to uncovering unknown values of ‘x’ that satisfy the equation. In this article, we embark on a journey to demystify this equation, providing insights and techniques to solve it effectively.
Understanding the Equation X2-11X+28=0
The equation X2-11X+28=0 is a quadratic equation, characterized by the presence of a squared term (x²) and two linear terms (-11x and +28). Quadratic equations commonly appear in various branches of mathematics, physics, and engineering, making them essential to understand and solve.
Read Also Scalp Massagers: Gimmick or Genuine Hair Care Tool?
Solving the Equation
To solve x² – 11x + 28 = 0, we can employ various methods, including factoring, completing the square, or using the quadratic formula. Let’s delve into each method briefly:
Factoring
Factoring involves breaking down the quadratic expression into its constituent factors. For our equation, we look for two numbers that multiply to 28 and add up to -11. These numbers are -4 and -7. Thus, we can rewrite the equation as (x – 4)(x – 7) = 0. Setting each factor to zero yields the solutions x = 4 and x = 7.
2. Completing the Square
Completing the square is another method to solve quadratic equations. By manipulating the equation to a perfect square trinomial form, we can easily find the solutions. However, this method might be more tedious compared to factoring.
3. Quadratic Formula
The quadratic formula, -b ± √(b² – 4ac) / 2a, offers a systematic approach to solve quadratic equations. Here, ‘a’, ‘b’, and ‘c’ represent the coefficients of the quadratic equation. Substituting the values from x² – 11x + 28 = 0 into the formula will yield the solutions directly.
Conclusion
In conclusion, the equation X2-11X+28=0 is a classic example of a quadratic equation, holding significance in mathematical problem-solving. By employing various techniques such as factoring, completing the square, or using the quadratic formula, we can unravel its solutions effectively. Understanding and mastering the art of solving such equations not only enriches our mathematical prowess but also enhances our problem-solving skills across different domains.
Unlocking the solutions to x² – 11x + 28 = 0 opens doors to a deeper understanding of quadratic equations and their applications, underscoring their importance in both theoretical and practical contexts.
FAQs
1. What does x² – 11x + 28 = 0 represent?
x² – 11x + 28 = 0 is a quadratic equation. It represents a mathematical expression involving a squared term (x²), a linear term (-11x), and a constant term (+28) equated to zero. Solving this equation helps in finding the values of ‘x’ that satisfy it.
2. Why is solving quadratic equations important?
Quadratic equations appear in various fields such as physics, engineering, economics, and more. Solving them helps in analyzing real-life scenarios involving motion, optimization, and equilibrium. Additionally, quadratic equations serve as foundational knowledge for more complex mathematical concepts.
3. What are the different methods to solve x² – 11x + 28 = 0?
There are several methods to solve quadratic equations, including factoring, completing the square, and using the quadratic formula. Factoring involves breaking down the expression into its constituent factors. Completing the square involves transforming the equation into a perfect square trinomial form. The quadratic formula provides a direct way to find the solutions of a quadratic equation.
4. How can I determine which method to use for solving x² – 11x + 28 = 0?
The choice of method depends on factors such as the complexity of the equation and personal preference. If the equation is easily factorable, factoring might be the simplest method. Completing the square is useful for equations that are not easily factorable, while the quadratic formula is a general method applicable to all quadratic equations.
5. Are there any applications of x² – 11x + 28 = 0 in real life?
Yes, quadratic equations like x² – 11x + 28 = 0 have numerous real-life applications. For instance, they are used in physics to describe the motion of projectiles, in economics to model profit and cost functions, and in engineering for optimization problems.
6. How can I check if my solutions to x² – 11x + 28 = 0 are correct?
You can verify your solutions by substituting them back into the original equation and confirming if it holds true. If the substituted values satisfy the equation, then they are indeed the correct solutions. Additionally, graphing the equation and observing the points of intersection with the x-axis can also confirm the solutions graphically.
7. Are there any advanced techniques for solving quadratic equations?
Yes, besides the standard methods mentioned, there are more advanced techniques like using the discriminant to determine the nature of solutions or employing numerical methods such as Newton’s method for finding approximate solutions. These techniques are particularly useful for complex equations or when exact solutions are difficult to obtain algebraically.